Approximate Nearest Neighbors Algorithms and Libraries

Introduction

Approximate nearest neighbor or ANN is a critical problem in Machine Learning and has numerous applications in various fields. The importance of ANN search lies in its ability to efficiently find approximate solutions to the nearest neighbor problem, which can lead to significant speedups and memory savings compared to the exact nearest neighbor search. There is obviously a trade-off decision between the accuracy of the approximate results and the time spent on calculation. In some tasks, the dataset is so huge that a fully accurate search is even impossible in a reasonable time, in others the difference between the accurate nearest neighbor and the approximate neighbor that is close can be not noticeable. ANN is being used in various applications:

1. Computer Vision: object recognition, image retrieval, and image stitching. It can efficiently match features in images or find images with similar visual content, enabling tasks like image matching and image recognition;

2. Information Retrieval: search engines, document retrieval. ANN search can be used to find similar documents or retrieve documents with similar content, enabling tasks like document retrieval, text similarity analysis, and content-based recommendation;

3. Recommendation Systems: ANN algorithms play a crucial role in tasks such as movie, product, and personalized content recommendations. It can find similar users or items based on their features or behaviour, enabling tasks like collaborative filtering, content-based filtering, and hybrid recommendation systems;

4. Computational Biology: protein folding, DNA sequence alignment, and drug discovery. ANN search can identify similar biological sequences or structures and be used for tasks like sequence alignment, and drug target identification.

In this article, I would like to cover the most popular algorithms and libraries for Approximate nearest neighbors search.

HNSW

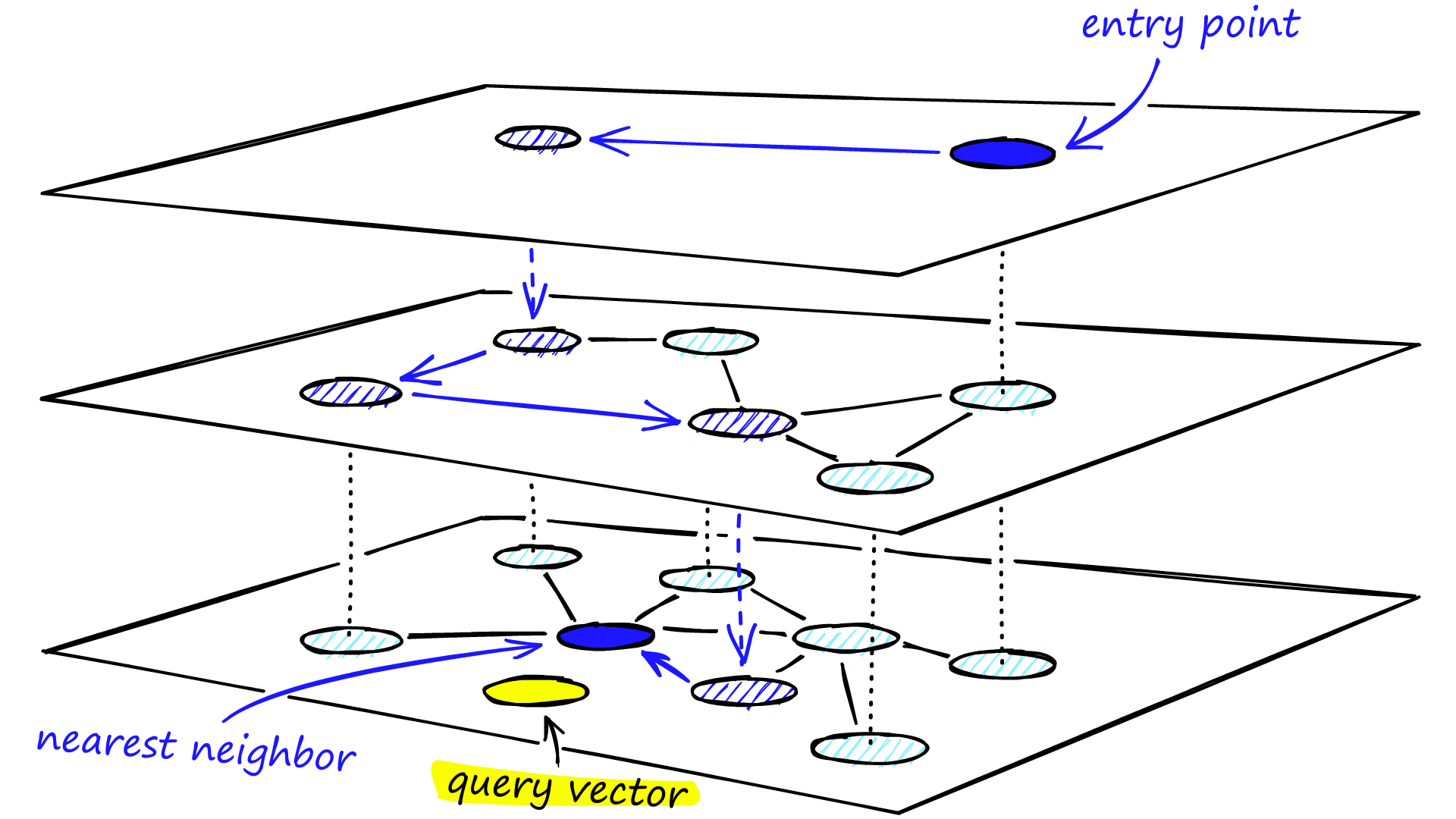
The original (parent algorithm) Navigable Small World (NSW) was introduced in 2011, and the more extended version, its successor, Hierarchical Navigable Small World (HNSW) appeared was published in 2016. It is based on the small world concept, which refers to a property of graphs where each node has short-range connections to its neighbors (approximately log(N) steps), but also has a few long-range connections that allow for efficient global exploration. HNSW algorithm builds a multi-layer hierarchical graph structure to efficiently index and search for nearest neighbors in high-dimensional spaces. Such graphs are quite common in real-world applications.

The key steps of the HNSW algorithm are:

1. Building the Graph Structure: algorithm starts by constructing a hierarchical graph structure with multiple layers. The first layer consists of the original data points, which are randomly assigned to nodes and each subsequent layer is built on top of the previous one by connecting nodes based on their proximity in the embedding space. Connections are made in a way that preserves the small-world property;

2. Navigating the Graph: during the search (inference) process, the algorithm starts from the top layer and traverses the graph by following the connections that bring it closer to the query point. At each layer, the algorithm selects a set of candidate nodes that are likely to contain the nearest neighbors based on their proximity to the query point. The number of candidates is controlled by a user which determines the trade-off between search efficiency and accuracy;

3. Adding and Removing Nodes: algorithm also supports dynamic updates (addition or removal of data points) without rebuilding the entire graph.

Overall, the HNSW algorithm is designed to efficiently handle high-dimensional data and can scale well to large datasets. In addition to it, the algorithm is flexible and adaptable to changing data distributions or data updates, making it suitable for dynamic environments. However, it requires tuning several parameters, such as the number of layers, the number of connections per node, and the parameter that controls the number of candidate nodes during the search. Apart from that, HNSW requires storing the graph structure in memory, which can result in significant memory overhead: the memory requirements increase with the number of layers and the number of connections per node, which may limit its scalability for datasets with limited memory resources.

Faiss

FAISS (Facebook AI Similarity Search) is a powerful and efficient open-source library developed by Facebook Research for similarity search and nearest neighbor search in large-scale datasets that was introduced in 2017. The library provides a range of algorithms that are optimized for different use cases and data characteristics, making it a popular choice for various applications in computer vision, natural language processing, recommendation systems, and other areas.

The main idea behind FAISS is to accelerate the search for nearest neighbors in a large dataset by exploiting the characteristics of high-dimensional data. Traditional methods like brute-force search or K-D trees can be slow and memory-intensive for high-dimensional data, while the FAISS library offers algorithms specifically designed for efficient similarity search in high-dimensional spaces.

FAISS offers several algorithms, including:

1. Flat is the simplest and most basic algorithm for similarity search. It represents the dataset as a flat list of vectors and performs a brute-force search to find the nearest neighbors. While being straightforward, it may not be the most efficient option for large datasets or high-dimensional data;

2. IVF (Inverted File) builds an inverted index of the dataset, where each entry in the index corresponds to a cluster of vectors. During the search, the algorithm only needs to visit a subset of clusters, which greatly reduces the search time compared to brute-force search;

3. Indexes for Dense or Sparse Vectors: FAISS provides specialized indexes for dense vectors (e.g., image embeddings) and sparse vectors (e.g., text embeddings) to optimize the search performance for different data types.

FAISS also offers advanced features such as multi-GPU support, multi-probe search, and customizable scoring functions, which allow users to fine-tune the search performance based on their specific requirements. Overall, it's a powerful and well-maintained library that provides customizable and efficient similarity search algorithms. As for the main drawbacks of the library, it's not very fast, from my experiments, it was 3-4 times slower than HNSW on CPU, also, some algorithms may require preprocessing of data, which may add additional overhead in data preparation.

Annoy

The Annoy (Approximate Nearest Neighbors Oh Yeah!) was developed by Erik Bernhardsson at Spotify and is widely used in various applications that require fast and scalable similarity search. The Annoy algorithm is based on the concept of constructing a hierarchical tree structure, known as an Annoy tree, that organizes data points in a way that allows for efficient approximate nearest neighbor search.

Here are the main steps of Annoy algorithm:

1. Indexing: take the input dataset of data points and randomly select a splitting point along a randomly chosen dimension to create the root node of the Annoy tree. The data points are then recursively partitioned into smaller regions by randomly selecting splitting points along different dimensions at each level of the tree. Splitting points are chosen in a way that tries to evenly distribute the data points across the tree, aiming for a balanced tree structure;

1. Balancing: during the construction of the Annoy tree, the algorithm ensures that the tree is balanced by maintaining a maximum allowed size for each node. If the number of data points in a node exceeds the maximum allowed size, the node is split into two child nodes by choosing a new splitting point along a random dimension. This process continues recursively until all the leaf nodes in the tree are created;

1. Querying: algorithm starts at the root node of the tree, the query point is compared to the splitting point of the current node along the chosen dimension, and based on the comparison, the algorithm chooses the child node that is closer to the query point. The process continues recursively as the algorithm navigates down the tree by choosing the child node that is closer to the query point until a leaf node is reached;

1. Approximate results: once a leaf node is reached, the algorithm retrieves the data points stored in that node as the initial set of approximate nearest neighbors. The algorithm then refines the approximate results by performing a brute-force search within a limited radius around the query point in the leaf node. The radius is determined by the maximum distance between the query point and the approximate nearest neighbors found so far, and the algorithm updates the approximate nearest neighbors with any closer points found during the radius search.

Annoy can handle large datasets with millions or even billions of data points, making it suitable for big data applications. It's very customizable: the library supports multiple distance metrics, making it adaptable to different use cases. As for drawbacks, Annoy uses randomization during the indexing process, which can result in different tree structures and search results for different runs, making the algorithm non-deterministic. Originally, the algorithm is optimized for static datasets and may require rebuilding the index from scratch when new data points are added or existing data points are updated, which can be time-consuming for dynamic datasets.

FLANN

FLANN (Fast Library for Approximate Nearest Neighbors) is an open-source library that provides fast and memory-efficient implementations of approximate nearest neighbor search algorithms. It is designed to efficiently search for nearest neighbors in high-dimensional data, making it suitable for a wide range of applications, such as CV, NLP, recommendation systems, and more.

FLANN supports multiple approximate nearest neighbor search algorithms, including KD-tree, Hierarchical Clustering, and Locality Sensitive Hashing (LSH), among others. The key feature is automatical choosing the best algorithm and optimum parameters depending on the dataset. FLANN is written in C++ and contains bindings for the following languages: C, MATLAB, Python, and Ruby.

One potential drawback of the FLANN is that it has not been actively maintained and updated since 2014. This lack of regular updates may pose potential issues with compatibility, bug fixes, and performance improvements in the future. As technology and requirements evolve, this may limit the library's ability to adapt to new environments or address potential issues that may arise. You may need to carefully consider the stability and support of the library before incorporating it into your projects, and be prepared to address any potential maintenance or compatibility issues that may arise in the future.

Conclusion and benchmarks

There is usually a trade-off between latency and recall for most of the ANN algorithms. It would be very hard to compare the algorithms with each other. The team of developers is maintaining and extending the benchmark of more than 20 ANN algorithms and libraries and testing them against multiple datasets. They also have an amazing interactive website with all plots. The key trade-off metrics that they take into account are Queries per second and Recall. Also, there are 13 datasets in the benchmark at the moment, so you can find the closest dataset to your task to make some conclusions about the most preferable approach.

In conclusion, Approximate Nearest Neighbor (ANN) algorithms are powerful tools for efficient and scalable nearest neighbor searches in a wide range of applications. ANN algorithms continue to be actively researched and developed, with advancements in indexing techniques, query processing, and hardware optimizations. As the field of machine learning continues to evolve and the amount of data in our world exponentially grows, ANN algorithms are expected to play a critical role in enabling efficient and scalable nearest neighbor search in a wide range of applications.